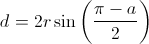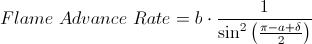To do this I create a mental feedback loop to increase the angle from vertical when the match flame is too small, and to decrease it when the flame is too large. In this post, I'd like to explore that feedback loop.
To begin, lets define some geometry. We'll assume the match is 1 dimensional, and has its origin at the head of the match, with the x dimension increasing as you move away from the head. As the flame progresses along the match, the flame has a front, which we define as the location of the first bit of unburnt match you can see next to the flame, and a rear, which is unburning char.
Additionally, we'll define the angle that the match is held from the vertical as 'a':
Now we can start to model the system. We'll make some simplifying assumptions:
1) once a section of match is lit, it will burn for a constant amount of time, regardless of the angle 'a'.
2) unburnt wood pyrolyzes at a rate inversely proportional to the square of the distance from the flame
We need to understand the relationship between the angle at which the match is held, and the characteristic distance between the flame and the unburnt part of the match:
we use the expression for the chord of a circle:
where r is a characteristic size of the flame, which we'll assume to be constant. The flame advance rate is then:
where b is the overall constant of proportionality, and delta is an offset that accounts for the thickness of the match. To get the experimental constants, we'll measure the rate of progression up the match, and fit a curve to the data. Here are the experiments:
Flame progression with match at 90 degrees:
With match at 125 degrees
With match close to 180 degrees:
And with match at about 60 degrees.
From these experiments we can make charts of the progression of the flame front and rear:
In these images the vertical distance between the two lines is the size of the flame at any given point in time, and the horizontal distance between the lines is the time it takes any given point along the match to ignite, burn, and extinguish itself.
The flame rate is the average slope of the 'front' curve in each image before it reaches the end of the match. We can plot these data points and fit a curve based upon the theoretical equations above, and solve for the experimental parameters 'b' ~ .025 and 'delta' ~ 20 degrees:
Now of course, these parameters are unique to our matches, in our environment, and will probably need to change with the circumstances, but this is at least enough to get us started.
From the graphs of our experiments we also estimate the time a given part of the match spends burning as about 5 seconds, and the minimum flame size to sustain burning as 3/16ths of an inch. Its not important for us to be super precise, as we'll be looking at trends and behaviors in our model, and because each type of match will behave differently.
In the next post on this topic, we'll build a model of our system using the parameters we estimated here, and see if we can recreate the observed behavior.